fastjet::SearchTree< T > Class Template Reference

This is the class for a search tree designed to be especially efficient when looking for successors and predecessors (to be used in Chan's CP algorithm). More...

#include <SearchTree.hh>

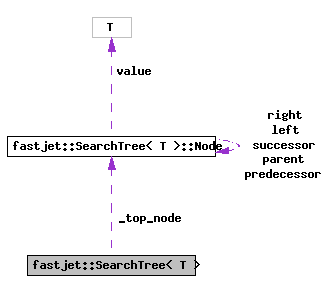
Collaboration diagram for fastjet::SearchTree< T >:

[legend]List of all members.

Public Member Functions
	SearchTree (const std::vector< T > &init)
	initialise from a sorted initial array
	SearchTree (const std::vector< T > &init, unsigned int max_size)
	initialise from a sorted initial array allowing for a larger maximum size of the array.
void	remove (unsigned node_index)
	remove the node corresponding to node_index from the search tree
void	remove (SearchTree::Node *node)
void	remove (SearchTree::circulator &circ)
circulator	insert (const T &value)
	insert the supplied value into the tree and return a pointer to the relevant SearchTreeNode.
const Node &	operator[] (int i) const
unsigned int	size () const
	return the number of elements currently in the search tree
void	verify_structure ()
	check that the structure we've obtained makes sense...
void	verify_structure_linear () const
void	verify_structure_recursive (const Node *, const Node *, const Node *) const
void	print_elements ()
	print out all elements...
unsigned int	max_depth () const
int	loc (const Node *node) const
Node *	_find_predecessor (const Node *)
	return predecessor by walking through the tree
Node *	_find_successor (const Node *)
	return successor by walking through the tree
const Node &	operator[] (unsigned int i) const
const_circulator	somewhere () const
	return a circulator to some place in the tree (with a circulator you don't care where.
circulator	somewhere ()
Private Member Functions
void	_initialize (const std::vector< T > &init)
	do the actual hard work of initialization
void	_do_initial_connections (unsigned int this_one, unsigned int scale, unsigned int left_edge, unsigned int right_edge, unsigned int depth)
	Recursive creation of connections, assuming the _nodes vector is completely filled and ordered.
Private Attributes
std::vector< Node >	_nodes
std::vector< Node * >	_available_nodes
Node *	_top_node
unsigned int	_n_removes
Classes
class	circulator
class	const_circulator
class	Node

---

Detailed Description

template<class T>
class fastjet::SearchTree< T >

This is the class for a search tree designed to be especially efficient when looking for successors and predecessors (to be used in Chan's CP algorithm).

It has the requirement that the maximum size of the search tree must be known in advance.

Definition at line 48 of file SearchTree.hh.

---

Constructor & Destructor Documentation

template<class T>

fastjet::SearchTree< T >::SearchTree

(

const std::vector< T > &

init

)

[inline]

initialise from a sorted initial array

Definition at line 304 of file SearchTree.hh.

References fastjet::SearchTree< T >::_available_nodes, and fastjet::SearchTree< T >::_initialize().

                                                                     :
  _nodes(init.size()), _available_nodes(0) {

  // reserve space for the list of available nodes
  _available_nodes.reserve(init.size());
  _initialize(init);
}

template<class T>

fastjet::SearchTree< T >::SearchTree	(	const std::vector< T > &	init,
		unsigned int	max_size
	)			[inline]

initialise from a sorted initial array allowing for a larger maximum size of the array.

..

Definition at line 289 of file SearchTree.hh.

References fastjet::SearchTree< T >::_available_nodes, fastjet::SearchTree< T >::_initialize(), and fastjet::SearchTree< T >::_nodes.

                                                                   :
  _nodes(max_size) {

  _available_nodes.reserve(max_size);
  _available_nodes.resize(max_size - init.size());
  for (unsigned int i = init.size(); i < max_size; i++) {
    _available_nodes[i-init.size()] = &(_nodes[i]);
  }

  _initialize(init);
}

---

Member Function Documentation

template<class T>

void fastjet::SearchTree< T >::remove

(

unsigned

node_index

)

remove the node corresponding to node_index from the search tree

template<class T>

void fastjet::SearchTree< T >::remove

(

SearchTree< T >::Node *

node

)

template<class T>

void fastjet::SearchTree< T >::remove

(

SearchTree< T >::circulator &

circ

)

[inline]

Definition at line 436 of file SearchTree.hh.

References fastjet::SearchTree< T >::circulator::_node.

                                                              {
  remove(circ._node);
}

template<class T>

SearchTree< T >::circulator fastjet::SearchTree< T >::insert

(

const T &

value

)

[inline]

insert the supplied value into the tree and return a pointer to the relevant SearchTreeNode.

Definition at line 536 of file SearchTree.hh.

References fastjet::SearchTree< T >::_available_nodes, fastjet::SearchTree< T >::_find_predecessor(), fastjet::SearchTree< T >::_find_successor(), fastjet::SearchTree< T >::_top_node, fastjet::SearchTree< T >::Node::left, fastjet::SearchTree< T >::Node::parent, fastjet::SearchTree< T >::Node::predecessor, fastjet::SearchTree< T >::Node::right, and fastjet::SearchTree< T >::Node::value.

                                                                                        {
  // make sure we don't exceed allowed number of nodes...
  assert(_available_nodes.size() > 0);

  Node * node = _available_nodes.back();
  _available_nodes.pop_back();
  node->value = value;

  Node * location = _top_node;
  Node * old_location = NULL;
  bool             on_left = true; // (init not needed -- but soothes g++4)
  // work through tree until we reach its end
#ifdef TRACK_DEPTH
  unsigned int depth = 0;
#endif
  while(location != NULL) {
#ifdef TRACK_DEPTH
    depth++;
#endif
    old_location = location;
    on_left = value < location->value;
    if (on_left) {location = location->left;}
    else {location = location->right;}
  }
#ifdef TRACK_DEPTH
  _max_depth = max(depth, _max_depth);
#endif
  // now create tree links
  node->parent = old_location;
  if (on_left) {node->parent->left = node;} 
  else {node->parent->right = node;}
  node->left = NULL;
  node->right = NULL;
  // and create predecessor / successor links
  node->predecessor = _find_predecessor(node);
  if (node->predecessor != NULL) {
    // it exists, so make use of its info (will include a cyclic case,
    // when successor is round the bend)
    node->successor = node->predecessor->successor;
    node->predecessor->successor = node;
    node->successor->predecessor = node;
  } else {
    // deal with case when we are left-most edge of tree (then successor
    // will exist...)
    node->successor = _find_successor(node);
    assert(node->successor != NULL); // can only happen if we're sole element 
                                     // (but not allowed, since tree size>=1)
    node->predecessor = node->successor->predecessor;
    node->successor->predecessor = node;
    node->predecessor->successor = node;
  }

  return circulator(node);
}

template<class T>

const Node& fastjet::SearchTree< T >::operator[]

(

int

i

)

const [inline]

Definition at line 72 of file SearchTree.hh.

{return _nodes[i];};

template<class T>

unsigned int fastjet::SearchTree< T >::size

(

)

const [inline]

return the number of elements currently in the search tree

Definition at line 75 of file SearchTree.hh.

Referenced by fastjet::SearchTree< T >::verify_structure_linear().

{return _nodes.size() - _available_nodes.size();}

template<class T>

void fastjet::SearchTree< T >::verify_structure

(

)

[inline]

check that the structure we've obtained makes sense...

Definition at line 593 of file SearchTree.hh.

References fastjet::SearchTree< T >::_top_node, fastjet::SearchTree< T >::Node::left, fastjet::SearchTree< T >::Node::right, fastjet::SearchTree< T >::verify_structure_linear(), and fastjet::SearchTree< T >::verify_structure_recursive().

                                                       {
  
  // do a check running through all elements
  verify_structure_linear();

  // do a recursive check down tree from top

  // first establish the extremities
  const Node * left_limit = _top_node;
  while (left_limit->left != NULL) {left_limit = left_limit->left;}
  const Node * right_limit = _top_node;
  while (right_limit->right != NULL) {right_limit = right_limit->right;}

  // then actually do recursion
  verify_structure_recursive(_top_node, left_limit, right_limit);
}

template<class T>

void fastjet::SearchTree< T >::verify_structure_linear

(

)

const [inline]

Definition at line 638 of file SearchTree.hh.

References fastjet::SearchTree< T >::_available_nodes, fastjet::SearchTree< T >::_nodes, and fastjet::SearchTree< T >::size().

Referenced by fastjet::SearchTree< T >::verify_structure().

                                                                    {

  //print_elements();

  unsigned n_top = 0;
  unsigned n_null = 0;
  for(unsigned i = 0; i < _nodes.size(); i++) {
    const typename SearchTree<T>::Node * node = &(_nodes[i]);
    // make sure node is defined
    if (node->treelinks_null()) {n_null++; continue;}

    // make sure of the number of "top" nodes 
    if (node->parent == NULL) {
      n_top++;
      //assert(node->left != NULL);
      //assert(node->right != NULL);
    } else {
      // make sure that I am a child of my parent...
      //assert((node->parent->left == node) || (node->parent->right == node));
      assert((node->parent->left == node) ^ (node->parent->right == node));
    }

    // when there is a left child make sure it's value is ordered
    // (note use of !(b<a), to allow for a<=b while using just the <
    // operator)
    if (node->left != NULL) {
      assert(!(node->value < node->left->value ));}

    // when there is a right child make sure it's value is ordered
    if (node->right != NULL) {
      assert(!(node->right->value < node->value ));}

  }
  assert(n_top == 1 || (n_top == 0 && size() <= 1) );
  assert(n_null == _available_nodes.size() ||
         (n_null == _available_nodes.size() + 1 && size() == 1));
}

template<class T>

void fastjet::SearchTree< T >::verify_structure_recursive	(	const Node *	,
		const Node *	,
		const Node *
	)			const

Referenced by fastjet::SearchTree< T >::verify_structure().

template<class T>

void fastjet::SearchTree< T >::print_elements

(

)

[inline]

print out all elements...

Definition at line 727 of file SearchTree.hh.

References fastjet::SearchTree< T >::_nodes, and fastjet::SearchTree< T >::loc().

                                                     {
  typename SearchTree<T>::Node * base_node = &(_nodes[0]);
  typename SearchTree<T>::Node * node = base_node;
  
  int n = _nodes.size();
  for(; node - base_node < n ; node++) {
    printf("%4d parent:%4d left:%4d right:%4d pred:%4d succ:%4d value:%10.6f\n",loc(node), loc(node->parent), loc(node->left), loc(node->right), loc(node->predecessor),loc(node->successor),node->value);
  }
}

template<class T>

unsigned int fastjet::SearchTree< T >::max_depth

(

)

const [inline]

Definition at line 91 of file SearchTree.hh.

{return 0;};

template<class T>

int fastjet::SearchTree< T >::loc

(

const Node *

node

)

const [inline]

Definition at line 358 of file SearchTree.hh.

References fastjet::SearchTree< T >::_nodes.

Referenced by fastjet::SearchTree< T >::print_elements().

                                                                        {return node == NULL? 
      -999 : node - &(_nodes[0]);}

template<class T>

Node* fastjet::SearchTree< T >::_find_predecessor

(

const Node *

)

return predecessor by walking through the tree

Referenced by fastjet::SearchTree< T >::insert().

template<class T>

Node* fastjet::SearchTree< T >::_find_successor

(

const Node *

)

return successor by walking through the tree

Referenced by fastjet::SearchTree< T >::insert().

template<class T>

const Node& fastjet::SearchTree< T >::operator[]

(

unsigned int

i

)

const [inline]

Definition at line 101 of file SearchTree.hh.

{return _nodes[i];};

template<class T>

SearchTree< T >::const_circulator fastjet::SearchTree< T >::somewhere

(

)

const [inline]

return a circulator to some place in the tree (with a circulator you don't care where.

..)

Definition at line 744 of file SearchTree.hh.

References fastjet::SearchTree< T >::_top_node.

                                                                                        {
  return const_circulator(_top_node);
}

template<class T>

SearchTree< T >::circulator fastjet::SearchTree< T >::somewhere

(

)

[inline]

Definition at line 738 of file SearchTree.hh.

References fastjet::SearchTree< T >::_top_node.

                                                                            {
  return circulator(_top_node);
}

template<class T>

void fastjet::SearchTree< T >::_initialize

(

const std::vector< T > &

init

)

[inline, private]

do the actual hard work of initialization

Definition at line 314 of file SearchTree.hh.

References fastjet::SearchTree< T >::_do_initial_connections(), fastjet::SearchTree< T >::_n_removes, fastjet::SearchTree< T >::_nodes, and fastjet::SearchTree< T >::_top_node.

Referenced by fastjet::SearchTree< T >::SearchTree().

                                                                           {

  _n_removes = 0;
  unsigned n = init.size();
  assert(n>=1);

  // reserve space for the list of available nodes
  //_available_nodes.reserve();

#ifdef TRACK_DEPTH
  _max_depth     = 0;
#endif


  // validate the input
  for (unsigned int i = 1; i<n; i++) {
    assert(!(init[i] < init[i-1]));
  }
  
  // now initialise the vector; link neighbours in the sequence
  for(unsigned int i = 0; i < n; i++) {
    _nodes[i].value = init[i];
    _nodes[i].predecessor = (& (_nodes[i])) - 1;
    _nodes[i].successor   = (& (_nodes[i])) + 1;
    _nodes[i].nullify_treelinks();
  }
  // make a loop structure so that we can circulate...
  _nodes[0].predecessor = (& (_nodes[n-1]));
  _nodes[n-1].successor = (& (_nodes[0]));

  // now label the rest of the nodes
  unsigned int scale = (n+1)/2;
  unsigned int top   = std::min(n-1,scale);
  _nodes[top].parent = NULL;
  _top_node = &(_nodes[top]);
  _do_initial_connections(top, scale, 0, n, 0);

  // make sure things are sensible...
  //verify_structure();
}

template<class T>

void fastjet::SearchTree< T >::_do_initial_connections	(	unsigned int	this_one,
		unsigned int	scale,
		unsigned int	left_edge,
		unsigned int	right_edge,
		unsigned int	depth
	)			[inline, private]

Recursive creation of connections, assuming the _nodes vector is completely filled and ordered.

Assumes this_one's parent is labelled, and was generated at a scale "scale" -- connections will be carried out including left edge and excluding right edge

Definition at line 365 of file SearchTree.hh.

References fastjet::SearchTree< T >::_nodes.

Referenced by fastjet::SearchTree< T >::_initialize().

                                           {

#ifdef TRACK_DEPTH
  // keep track of tree depth for checking things stay reasonable...
  _max_depth = max(depth, _max_depth);
#endif

  //std::cout << this_one << " "<< scale<< std::endl;
  unsigned int ref_new_scale = (scale+1)/2;

  // work through children to our left
  unsigned new_scale = ref_new_scale;
  bool     did_child  = false;
  while(true) {
    int left = this_one - new_scale; // be careful here to use signed int...
    // if there is something unitialised to our left, link to it
    if (left >= static_cast<int>(left_edge) 
                        && _nodes[left].treelinks_null() ) {
      _nodes[left].parent = &(_nodes[this_one]);
      _nodes[this_one].left = &(_nodes[left]);
      // create connections between left_edge and this_one
      _do_initial_connections(left, new_scale, left_edge, this_one, depth+1);
      did_child = true;
      break;
    }
    // reduce the scale so as to try again
    unsigned int old_new_scale = new_scale;
    new_scale = (old_new_scale + 1)/2;
    // unless we've reached end of tree
    if (new_scale == old_new_scale) break;
  }
  if (!did_child) {_nodes[this_one].left = NULL;}


  // work through children to our right
  new_scale = ref_new_scale;
  did_child  = false;
  while(true) {
    unsigned int right = this_one + new_scale;
    if (right < right_edge  && _nodes[right].treelinks_null()) {
      _nodes[right].parent = &(_nodes[this_one]);
      _nodes[this_one].right = &(_nodes[right]);
      // create connections between this_one+1 and right_edge
      _do_initial_connections(right, new_scale, this_one+1,right_edge,depth+1);
      did_child = true;
      break;
    }
    // reduce the scale so as to try again
    unsigned int old_new_scale = new_scale;
    new_scale = (old_new_scale + 1)/2;
    // unless we've reached end of tree
    if (new_scale == old_new_scale) break;
  }
  if (!did_child) {_nodes[this_one].right = NULL;}

}

---

Member Data Documentation

template<class T>

std::vector<Node> fastjet::SearchTree< T >::_nodes [private]

Definition at line 112 of file SearchTree.hh.

Referenced by fastjet::SearchTree< T >::_do_initial_connections(), fastjet::SearchTree< T >::_initialize(), fastjet::SearchTree< T >::loc(), fastjet::SearchTree< T >::print_elements(), fastjet::SearchTree< T >::SearchTree(), and fastjet::SearchTree< T >::verify_structure_linear().

template<class T>

std::vector<Node *> fastjet::SearchTree< T >::_available_nodes [private]

Definition at line 113 of file SearchTree.hh.

Referenced by fastjet::SearchTree< T >::insert(), fastjet::SearchTree< T >::SearchTree(), and fastjet::SearchTree< T >::verify_structure_linear().

template<class T>

Node* fastjet::SearchTree< T >::_top_node [private]

Definition at line 114 of file SearchTree.hh.

Referenced by fastjet::SearchTree< T >::_initialize(), fastjet::SearchTree< T >::insert(), fastjet::SearchTree< T >::somewhere(), and fastjet::SearchTree< T >::verify_structure().

template<class T>

unsigned int fastjet::SearchTree< T >::_n_removes [private]

Definition at line 115 of file SearchTree.hh.

Referenced by fastjet::SearchTree< T >::_initialize().

---

The documentation for this class was generated from the following file:

• include/fastjet/internal/SearchTree.hh

---